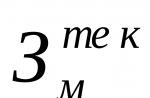Jepen: momentet e inercisë së figurës në lidhje me boshtet z, y; distancat ndërmjet këtyre dhe akseve paralele z 1, y 1 – a, b.
Përcaktoni: momentet e inercisë rreth boshteve z 1, y 1 (Fig. 4.7).
Koordinatat e çdo pike në sistemin e ri z 1 Oy 1 mund të shprehen përmes koordinatave në sistemin e vjetër si kjo:
z 1 = z + b, y 1 = y + a.
Ne i zëvendësojmë këto vlera në formulat (4.6) dhe (4.8) dhe integrojmë term pas termi:
Në përputhje me formulat (4.1) dhe (4.6), marrim
 ,
,
 , (4.13)
, (4.13)
Nëse të dhënat fillestare të boshtit zCy janë qendrore, atëherë momentet statike S z dhe
S y janë të barabartë me zero dhe formulat (4.13) janë thjeshtuar:
 ,
,
 , (4.14)
, (4.14)
 .
.
Shembull: përcaktoni momentin boshtor të inercisë së drejtkëndëshit në lidhje me boshtin z 1 që kalon përmes bazës (Fig. 4.6, a). Sipas formulës (4.14)
4.4. Varësia ndërmjet momenteve të inercisë gjatë rrotullimit të boshteve
Jepen: momentet e inercisë së një figure arbitrare në lidhje me boshtet koordinative z, y; këndi i rrotullimit të këtyre akseve α (Fig. 4.8). Ne e konsiderojmë këndin e rrotullimit në drejtim të kundërt të orës si pozitiv.
Përcaktoni: momentet e inercisë së figurës në raport me z 1, y 1.

Koordinatat e një zone elementare arbitrare dF në akset e reja shprehen përmes koordinatave të sistemit të mëparshëm të boshteve si më poshtë:
z 1 = OB = OE + EB = OE + DC = zcos α + ysin α,
y 1 = AB = AC – BC = AC – ED = ycos α – zsin α.
Le t'i zëvendësojmë këto vlera në (4.6) dhe (4.8) dhe t'i integrojmë term pas termi:
 ,
,
 ,
,

Duke marrë parasysh formulat (4.6) dhe (4.8), më në fund gjejmë:
 . (4.16)
. (4.16)
Duke shtuar formulat (4.15), marrim: (4.17)
Kështu, kur boshtet rrotullohen, shuma e momenteve boshtore të inercisë mbetet konstante. Në këtë rast, secila prej tyre ndryshon në përputhje me formulat (4.15). Është e qartë se në një pozicion të akseve momentet e inercisë do të kenë vlera ekstreme: njëri prej tyre do të jetë më i madhi, tjetri më i vogli.
4.5. Boshtet kryesore dhe momentet kryesore të inercisë
Akset kryesore qendrore, momenti centrifugal i inercisë rreth të cilit është zero, kanë rëndësinë më të madhe praktike. Akset e tilla do t'i shënojmë me shkronjat u, υ. Rrjedhimisht, J uυ = 0. Sistemi fillestar arbitrar i koordinatave z, y duhet të rrotullohet me një kënd të tillë α 0 që momenti centrifugal i inercisë të bëhet i barabartë me zero. Duke barazuar (4.16) me zero, marrim
 . (4.18)
. (4.18)
Rezulton se teoria e momenteve të inercisë dhe teoria e gjendjes së tensionit planor përshkruhen nga i njëjti aparat matematikor, pasi formula (4.15) - (4.18) janë identike me formulat (3.10), (3.11) dhe (3.18). Vetëm në vend të sforcimeve normale σ regjistrohen momente boshtore të inercisë J z dhe J y, dhe në vend të sforcimeve tangjenciale τ zy - momenti centrifugal i inercisë J zy. Prandaj, ne paraqesim formulat për momentet kryesore boshtore të inercisë pa derivim, në analogji me formulat (3.18):
 .(4.19)
.(4.19)
Dy vlerat e këndit α 0 të marra nga (4.18) ndryshojnë nga njëra-tjetra me 90 0, më e vogla nga këto kënde nuk i kalon 45 0 në vlerë absolute.
Rrezja e inercisë dhe momenti i rezistencës
Momenti i inercisë së një figure në lidhje me çdo bosht mund të përfaqësohet si produkt i sipërfaqes së figurës me katrorin e një sasie të caktuar, i quajtur rrezja e rrotullimit:
 , (4.20)
, (4.20)
ku i z është rrezja e rrotullimit në lidhje me boshtin z.
Nga shprehja (4.20) rezulton se
 ,
, . (4.21)
. (4.21)
Boshtet kryesore qendrore të inercisë korrespondojnë me rrezet kryesore të inercisë
 ,
, . (4.22)
. (4.22)
Duke ditur rrezet kryesore të inercisë, ju mund të gjeni grafikisht rrezen e inercisë (dhe, rrjedhimisht, momentin e inercisë) në lidhje me një bosht arbitrar.
Le të shqyrtojmë një karakteristikë tjetër gjeometrike që karakterizon forcën e shufrës gjatë rrotullimit dhe përkuljes - momenti i rezistencës. Momenti i rezistencës është i barabartë me momentin e inercisë të ndarë me distancën nga boshti (ose nga poli) deri në pikën më të largët të seksionit. Dimensioni i momentit të rezistencës është një njësi gjatësie në kub (cm 3).
Për një drejtkëndësh (Fig. 4.6, a)  ,
, , pra momentet aksiale të rezistencës
, pra momentet aksiale të rezistencës
 ,
, . (4.23)
. (4.23)
Për një rreth  (Fig. 4.6, b),
(Fig. 4.6, b),  , pra momenti polar i rezistencës
, pra momenti polar i rezistencës
 . (4.24)
. (4.24)
Për një rreth  ,
, , pra momenti aksial i rezistencës
, pra momenti aksial i rezistencës
 . (4.25)
. (4.25)
Le të prezantojmë një sistem koordinativ drejtkëndor kartezian O xy. Le të shqyrtojmë një seksion arbitrar (zone të mbyllur) me zonën A në rrafshin koordinativ (Fig. 1).
Momente statike

Pika C me koordinata (x C , y C)

thirrur qendra e gravitetit të seksionit.
Nëse boshtet e koordinatave kalojnë nëpër qendrën e gravitetit të seksionit, atëherë momentet statike të seksionit janë të barabarta me zero:
Momentet aksiale të inercisë seksionet në lidhje me boshtet x dhe y quhen integrale të formës:

Momenti polar i inercisë seksioni në lidhje me origjinën e koordinatave quhet një integral i formës:
![]()
Momenti centrifugal i inercisë seksioni quhet integral i formës:

Akset kryesore të inercisë së seksionit quhen dy boshte reciprokisht pingul, në raport me të cilin I xy = 0. Nëse një nga boshtet reciprokisht pingul është boshti i simetrisë së seksionit, atëherë I xy =0 dhe, për rrjedhojë, këto boshte janë kryesoret. Akset kryesore që kalojnë nëpër qendrën e gravitetit të seksionit quhen akset kryesore qendrore të inercisë së seksionit
2. Teorema Steiner-Huygens mbi përkthimin paralel të boshteve
Teorema Steiner-Huygens (teorema e Shtajnerit).
Momenti boshtor i inercisë së seksionit I në lidhje me një bosht fiks arbitrar x është i barabartë me shumën e momentit boshtor të inercisë të këtij seksioni I me boshtin relativ x * paralel me të, duke kaluar nëpër qendrën e masës së seksionit, dhe prodhimi i sipërfaqes së prerjes tërthore A me katrorin e distancës d ndërmjet dy boshteve.
![]()

Nëse momentet e inercisë I x dhe I y në lidhje me boshtet x dhe y janë të njohura, atëherë në lidhje me boshtet ν dhe u të rrotulluar nga një kënd α, momentet boshtore dhe centrifugale të inercisë llogariten duke përdorur formulat:

Nga formulat e mësipërme është e qartë se
![]()
Ato. shuma e momenteve boshtore të inercisë kur rrotullohen boshtet pingul reciprokisht nuk ndryshon, d.m.th. boshtet u dhe v, në lidhje me të cilat momenti centrifugal i inercisë së seksionit është zero, dhe momentet boshtore të inercisë I u dhe I v kanë ekstreme vlerat max ose min quhen boshtet kryesore të seksionit. Akset kryesore që kalojnë nëpër qendrën e gravitetit të seksionit quhen akset kryesore qendrore të seksionit. Për seksionet simetrike, boshtet e tyre të simetrisë janë gjithmonë boshtet kryesore qendrore. Pozicioni i akseve kryesore të seksionit në lidhje me akset e tjera përcaktohet duke përdorur marrëdhënien:

ku α 0 është këndi me të cilin boshtet x dhe y duhet të rrotullohen në mënyrë që ato të bëhen kryesore (një kënd pozitiv zakonisht vendoset në drejtim të kundërt, një kënd negativ vendoset në drejtim të akrepave të orës). Momentet boshtore të inercisë rreth boshteve kryesore quhen momentet kryesore të inercisë:
Shenja plus përpara termit të dytë i referohet momentit maksimal të inercisë, shenjës minus në minimum.
Boshtet që kalojnë nëpër qendrën e gravitetit të një figure të rrafshët quhen boshtet qendrore.
Momenti i inercisë rreth boshtit qendror quhet momenti qendror i inercisë.
Teorema
Momenti i inercisë rreth çdo boshti është i barabartë me shumën e momentit të inercisë rreth boshtit qendror paralel me atë të dhënë dhe produktin e sipërfaqes së figurës dhe katrorit të distancës midis boshteve.
Për të vërtetuar këtë teoremë, merrni parasysh një figurë të rrafshët arbitrare sipërfaqja e së cilës është e barabartë me A
, qendra e gravitetit ndodhet në pikën ME
, dhe momenti qendror i inercisë rreth boshtit x
do Unë x
.
Le të llogarisim momentin e inercisë së figurës në lidhje me një bosht të caktuar x 1
, paralel me boshtin qendror dhe i ndarë prej tij në një distancë A
(oriz).
I x1 = Σ y 1 2 dA + Σ (y + a) 2 dA =
= Σ y 2 dA + 2a Σ y dA + a 2 Σ dA.
Duke analizuar formulën që rezulton, vërejmë se termi i parë është momenti boshtor i inercisë në lidhje me boshtin qendror, termi i dytë është momenti statik i zonës së kësaj figure në lidhje me boshtin qendror (pra, është i barabartë me zero), dhe termi i tretë pas integrimit mund të përfaqësohet si produkt a 2 A , d.m.th., si rezultat marrim formulën:
I x1 = I x + a 2 A- vërtetohet teorema.
Bazuar në teoremën, mund të konkludojmë se në një seri boshtesh paralele, momenti boshtor i inercisë së një figure të sheshtë do të jetë më i vogli në raport me boshtin qendror .
Boshtet kryesore dhe momentet kryesore të inercisë
Le të imagjinojmë një figurë të sheshtë, momentet e inercisë së së cilës në lidhje me boshtet koordinative Unë x Dhe Unë y , dhe momenti polar i inercisë në lidhje me origjinën është i barabartë me I ρ . Siç u vendos më herët,
I x + I y = I ρ.
Nëse boshtet e koordinatave rrotullohen në planin e tyre rreth origjinës së koordinatave, atëherë momenti polar i inercisë do të mbetet i pandryshuar, dhe momentet boshtore do të ndryshojnë, ndërsa shuma e tyre do të mbetet konstante. Meqenëse shuma e variablave është konstante, njëri prej tyre zvogëlohet dhe tjetri rritet, dhe anasjelltas.
Rrjedhimisht, në një pozicion të caktuar të akseve, njëri prej momenteve boshtore do të arrijë vlerën maksimale, dhe tjetri - minimumin.
Boshtet rreth të cilave momentet e inercisë kanë vlera minimale dhe maksimale quhen boshtet kryesore të inercisë.
Momenti i inercisë rreth boshtit kryesor quhet momenti kryesor i inercisë.
Nëse boshti kryesor kalon nëpër qendrën e gravitetit të një figure, ai quhet boshti kryesor qendror, dhe momenti i inercisë rreth një boshti të tillë quhet momenti kryesor qendror i inercisë.
Mund të konkludojmë se nëse një figurë është simetrike për çdo bosht, atëherë ky bosht do të jetë gjithmonë një nga boshtet kryesore qendrore të inercisë së kësaj figure.
Momenti centrifugal i inercisë
Momenti centrifugal i inercisë së një figure të sheshtë është shuma e produkteve të zonave elementare të marra në të gjithë zonën dhe distanca në dy boshte reciprokisht pingul:
I xy = Σ xy dA,
Ku x
, y
- distancat nga vendi dA
te boshtet x
Dhe y
.
Momenti centrifugal i inercisë mund të jetë pozitiv, negativ ose zero.
Momenti centrifugal i inercisë përfshihet në formulat për përcaktimin e pozicionit të akseve kryesore të seksioneve asimetrike.
Tabelat standarde të profileve përmbajnë një karakteristikë të quajtur rrezja e rrotullimit të seksionit
, llogaritur me formulat:
i x = √ (I x / A),i y = √ (I y / A) , (në tekstin e mëtejmë shenja"√"- shenja e rrënjës)
Ku Unë x, unë y
- momentet aksiale të inercisë së seksionit në lidhje me akset qendrore; A
- sipërfaqja e prerjes tërthore.
Kjo karakteristikë gjeometrike përdoret në studimin e tensionit ose ngjeshjes ekscentrike, si dhe përkuljes gjatësore.
Deformim përdredhës
Konceptet themelore rreth rrotullimit. Përdredhje e një trau të rrumbullakët.
Përdredhja është një lloj deformimi në të cilin ndodh vetëm një çift rrotullues në çdo seksion kryq të rrezes, d.m.th. një faktor force që shkakton një lëvizje rrethore të seksionit në lidhje me një bosht pingul me këtë seksion, ose parandalon një lëvizje të tillë. Me fjalë të tjera, deformimet përdredhëse ndodhin nëse një palë ose çifte forcash aplikohen në një rreze të drejtë në plane pingul me boshtin e tij.
Momentet e këtyre çifteve të forcave quhen përdredhëse ose rrotulluese. Çift rrotullues shënohet me T
.
Ky përkufizim i ndan në mënyrë konvencionale faktorët e forcës së deformimit përdredhës në ata të jashtëm (përdredhës, çift rrotullues T
) dhe të brendshëm (çift rrotullues M kr
).
Në makina dhe mekanizma, boshtet e rrumbullakëta ose tuba i nënshtrohen më shpesh rrotullimit, kështu që llogaritjet e forcës dhe ngurtësisë bëhen më shpesh për njësi dhe pjesë të tilla.
Merrni parasysh rrotullimin e një boshti cilindrik rrethor.
Imagjinoni një bosht cilindrik gome në të cilin njëri nga skajet është i fiksuar fort, dhe në sipërfaqe ka një rrjet vijash gjatësore dhe rrathë tërthor. Ne do të zbatojmë disa forca në skajin e lirë të boshtit, pingul me boshtin e këtij boshti, d.m.th. do ta kthejmë atë përgjatë boshtit. Nëse shqyrtoni me kujdes linjat e rrjetës në sipërfaqen e boshtit, do të vini re se:
- boshti i boshtit, i cili quhet bosht i rrotullimit, do të mbetet i drejtë;
- diametrat e rrathëve do të mbeten të njëjta, dhe distanca midis rrathëve ngjitur nuk do të ndryshojë;
- vijat gjatësore në bosht do të kthehen në vija spirale.

Nga kjo mund të konkludojmë se kur një tra cilindrik i rrumbullakët (bosht) është i përdredhur, hipoteza e seksioneve të sheshta është e vlefshme dhe gjithashtu mund të supozojmë se rrezet e rrathëve mbeten drejt gjatë deformimit (pasi diametrat e tyre nuk kanë ndryshuar). Dhe meqenëse nuk ka forca gjatësore në seksionet e boshtit, distanca midis tyre ruhet.
Rrjedhimisht, deformimi rrotullues i një boshti të rrumbullakët konsiston në rrotullimin e seksioneve kryq në lidhje me njëri-tjetrin rreth boshtit të rrotullimit, dhe këndet e rrotullimit të tyre janë drejtpërdrejt proporcionale me distancat nga seksioni fiks - aq më larg çdo seksion nga fundi fiks. e boshtit, aq më i madh është këndi në lidhje me boshtin e boshtit që ai rrotullohet.
Për çdo seksion të boshtit, këndi i rrotullimit është i barabartë me këndin e rrotullimit të pjesës së boshtit të mbyllur midis këtij seksioni dhe vulës (fundi i fiksuar).
këndi ( oriz. 1) rrotullimi i skajit të lirë të boshtit (seksioni fundor) quhet këndi i plotë i rrotullimit të traut cilindrik (boshtit).
Këndi relativ i kthesës φ 0
quhet raporti i këndit të rrotullimit φ 1
në distancë l 1
nga një seksion i caktuar në embedment (seksion fiks).
Nëse trau cilindrik (boshti) është i gjatë l
ka një seksion kryq konstant dhe është i ngarkuar me një moment rrotullues në skajin e lirë (d.m.th., përbëhet nga një seksion gjeometrik homogjen), atëherë pohimi i mëposhtëm është i vërtetë:
φ 0 = φ 1 / l 1 = φ / l = konst
- vlera është konstante.
Nëse marrim parasysh një shtresë të hollë në sipërfaqen e shiritit cilindrik të gomës së mësipërme ( oriz. 1), i kufizuar nga një qelizë rrjeti cdef , atëherë vërejmë se kjo qelizë deformohet gjatë deformimit dhe ana e saj, e largët nga seksioni fiks, zhvendoset drejt kthesës së rrezes, duke zënë pozicionin cde 1 f 1 .
Duhet të theksohet se një pamje e ngjashme vërehet gjatë deformimit në prerje, vetëm në këtë rast sipërfaqja deformohet për shkak të lëvizjes përkthimore të seksioneve në raport me njëri-tjetrin, dhe jo për shkak të lëvizjes rrotulluese, si në deformimin përdredhës. Bazuar në këtë, mund të konkludojmë se gjatë rrotullimit në seksione tërthore, lindin vetëm forca të brendshme tangjenciale (sforcime), duke formuar një çift rrotullues.
Pra, çift rrotullimi është momenti që rezulton në lidhje me boshtin e rrezes së forcave të brendshme tangjenciale që veprojnë në seksion kryq.
Le të njihen edhe Ix, Iy, Ixy. Le të vizatojmë një bosht të ri x 1, y 1 paralel me boshtet xy.
Dhe le të përcaktojmë momentin e inercisë së të njëjtit seksion në lidhje me boshtet e reja.
X 1 = x-a; y 1 =y-b
I x 1 = ∫ y 1 dA = ∫ (y-b) 2 dA = ∫ (y 2 - 2by + b 3)dA = ∫ y 2 dA – 2b ∫ ydA + b 2 ∫dA=
Ix – 2b Sx + b 2 A.
Nëse boshti x kalon nëpër qendrën e gravitetit të seksionit, atëherë momenti statik Sx =0.
I x 1 = Ix + b 2 A
Ngjashëm me boshtin e ri y 1, do të kemi formulën I y 1 = Iy + a 2 A
Momenti centrifugal i inercisë rreth boshteve të reja
Ix 1 y 1 = Ixy – b Sx –a Sy + abA.
Nëse boshtet xy kalojnë nëpër qendrën e gravitetit të seksionit, atëherë Ix 1 y 1 = Ixy + abA
Nëse seksioni është simetrik, të paktën një nga boshtet qendrore përkon me boshtin e simetrisë, atëherë Ixy =0, që do të thotë Ix 1 y 1 = abA
Ndryshimi i momenteve të inercisë gjatë rrotullimit të boshteve.
Le të dihen momentet boshtore të inercisë rreth boshteve xy.
Ne marrim një sistem të ri të koordinatave xy duke rrotulluar sistemin e vjetër me një kënd (a > 0), nëse rrotullimi është në drejtim të kundërt të akrepave të orës.

Le të vendosim marrëdhënien midis koordinatave të vjetra dhe të reja të faqes
y 1 =ab = ac – bc = ab- de
nga trekëndëshi acd:
ac/ad =cos α ac= ad*cos α
nga trekëndëshi oed:
de/od =sin α dc = od*sin α
Le t'i zëvendësojmë këto vlera në shprehjen për y
y 1 = ad cos α - od sin α = y cos α - x sin α.
Po kështu
x 1 = x cos α + y sin α.
Le të llogarisim momentin boshtor të inercisë në lidhje me boshtin e ri x 1
Ix 1 = ∫y 1 2 dA = ∫ (y cos α - x sin α) 2 dA= ∫ (y 2 cos 2 α - 2xy sin α cos α + x 2 sin 2 α)dA= =cos 2 α ∫ y 2 dA – sin2 α ∫xy dA + sin 2 α ∫x 2 dA = Ix cos 2 α - Ixy sin2 α + Iy sin 2 α .
Në mënyrë të ngjashme, Iy 1 = Ix sin 2 α - Ixy sin2 α + Iy cos 2 α.
Le të shtojmë anën e majtë dhe të djathtë të shprehjeve që rezultojnë:
Ix 1 + Iy 1 = Ix (sin 2 α + cos 2 α) + Iy (sin 2 α + cos 2 α) + Ixy (sin2 α - cos2 α).
Ix 1 + Iy 1 = Ix + Iy
Shuma e momenteve boshtore të inercisë gjatë rrotullimit nuk ndryshon.
Le të përcaktojmë momentin centrifugal të inercisë në lidhje me boshtet e reja. Le të imagjinojmë vlerat x 1, y 1.
Ix 1 y 1 = ∫x 1 y 1 dA = (Ix – Iy)/2*sin 2 α + Ixy cos 2 α .
Momentet kryesore dhe boshtet kryesore të inercisë.
Momentet kryesore të inercisë ato quhen vlera ekstreme.
Akset rreth të cilave janë marrë vlerat ekstreme quhen boshtet kryesore të inercisë. Ata janë gjithmonë pingul reciprokisht.
Momenti centrifugal i inercisë në lidhje me boshtet kryesore është gjithmonë i barabartë me 0. Meqenëse dihet se ka një bosht simetrie në seksion, momenti centrifugal është i barabartë me 0, që do të thotë boshti i simetrisë është boshti kryesor. Nëse marrim derivatin e parë të shprehjes I x 1, atëherë e barazojmë me "0", fitojmë vlerën e këndit = që korrespondon me pozicionin e boshteve kryesore të inercisë.
tan2 α 0 = - ![]()
Nëse α 0 >0, atëherë për një pozicion të caktuar të akseve kryesore, boshti i vjetër duhet të rrotullohet në drejtim të kundërt të akrepave të orës. Një nga akset kryesore është max, dhe tjetri është min. Në këtë rast, boshti maksimal korrespondon gjithmonë me një kënd më të vogël me atë bosht të rastësishëm në lidhje me të cilin ai ka një moment boshtor më të madh të inercisë. Vlerat ekstreme të momentit boshtor të inercisë përcaktohen me formulën:
Kapitulli 2. Konceptet bazë të rezistencës së materialeve. Objektivat dhe metodat.
Gjatë projektimit të strukturave të ndryshme, është e nevojshme të zgjidhen çështje të ndryshme të forcës, ngurtësisë dhe stabilitetit.
Forcë– aftësia e një trupi të caktuar për të përballuar ngarkesa të ndryshme pa shkatërrim.
Ngurtësia– aftësia e një strukture për të thithur ngarkesa pa deformime (zhvendosje) të mëdha. Vlerat paraprake të lejuara të deformimit rregullohen nga kodet dhe rregulloret e ndërtimit (SNIP).
Qëndrueshmëria
Merrni parasysh ngjeshjen e një shufre fleksibël
Nëse ngarkesa rritet gradualisht, shufra së pari do të shkurtohet. Kur forca F arrin një vlerë të caktuar kritike, shufra do të shtrëngohet. - shkurtim absolut.
Në këtë rast, shufra nuk shembet, por ndryshon ashpër formën e saj. Ky fenomen quhet humbje e stabilitetit dhe çon në shkatërrim.
Sopromat- këto janë bazat e shkencave të forcës, ngurtësisë dhe qëndrueshmërisë së strukturave inxhinierike. Materialet e forcës përdorin metoda të mekanikës teorike, fizikës dhe matematikës. Ndryshe nga mekanika teorike, rezistenca e forcës merr parasysh ndryshimet në madhësinë dhe formën e trupave nën ndikimin e ngarkesës dhe temperaturës.
Le të përcaktojmë marrëdhënien midis momenteve të ndryshme të inercisë së seksionit në lidhje me dy boshtet paralele (Fig. 6.7), të lidhura nga varësitë

1. Për momentet statike të inercisë
Së fundi,
2. Për momentet boshtore të inercisë
prandaj,
Nëse boshti z kalon nëpër qendrën e gravitetit të seksionit, pastaj
Nga të gjitha momentet e inercisë rreth boshteve paralele, momenti boshtor i inercisë ka vlerën më të vogël rreth boshtit që kalon nëpër qendrën e gravitetit të seksionit.
E njëjta gjë për boshtin
Kur boshti y kalon nëpër qendrën e gravitetit të seksionit
3. Për momentet centrifugale të inercisë fitojmë
Më në fund mund të shkruajmë
Në rastin kur origjina e sistemit koordinativ yzështë në qendër të gravitetit të seksionit, marrim
Në rastin kur një ose të dy boshtet janë boshte simetrie,
6.7. Ndryshimi i momenteve të inercisë gjatë rrotullimit të boshteve
Le të jepen momentet e inercisë së seksionit në lidhje me boshtet koordinative z y.

Këndi konsiderohet pozitiv nëse sistemi i vjetër i koordinatave duhet të rrotullohet në drejtim të kundërt të akrepave të orës për të kaluar në atë të ri (për një sistem koordinativ drejtkëndor kartezian me dorën e djathtë). Të reja dhe të vjetra z y Sistemet e koordinatave janë të lidhura me varësi që vijojnë nga Fig. 6.8:
1. Le të përcaktojmë shprehjet për momentet boshtore të inercisë në lidhje me boshtet e sistemit të ri të koordinatave:
![]()
Po kështu në lidhje me boshtin
Nëse mbledhim vlerat e momenteve të inercisë rreth boshteve dhe, marrim
domethënë kur boshtet rrotullohen, shuma e momenteve boshtore të inercisë është një vlerë konstante.
2. Le të nxjerrim formulat për momentet centrifugale të inercisë.
![]() .
.
6.8. Momentet kryesore të inercisë. Boshtet kryesore të inercisë
Vlerat ekstreme të momenteve boshtore të inercisë së seksionit quhen momentet kryesore të inercisë.
Dy akset reciprokisht pingul, rreth të cilëve momentet boshtore të inercisë kanë vlera ekstreme, quhen boshtet kryesore të inercisë.
Për të gjetur momentet kryesore të inercisë dhe pozicionin e boshteve kryesore të inercisë, përcaktojmë derivatin e parë në lidhje me këndin e momentit të inercisë, të përcaktuar me formulën (6.27)
Le ta barazojmë këtë rezultat me zero:
ku është këndi me të cilin duhet të rrotullohen boshtet koordinative y Dhe z në mënyrë që ato të përkojnë me akset kryesore.
Duke krahasuar shprehjet (6.30) dhe (6.31), mund ta vërtetojmë atë
![]() ,
,
Rrjedhimisht, në lidhje me boshtet kryesore të inercisë, momenti centrifugal i inercisë është zero.
Akset reciproke pingule, një ose të dy prej të cilëve përkojnë me boshtet e simetrisë së seksionit, janë gjithmonë boshtet kryesore të inercisë.
Le të zgjidhim ekuacionin (6.31) për këndin:
![]() .
.
Nëse >0, atëherë për të përcaktuar pozicionin e njërit prej boshteve kryesore të inercisë për sistemin koordinativ drejtkëndor kartezian djathtas (majtas), nevojitet një bosht z kthehuni në një kënd kundër drejtimit të rrotullimit (në drejtim të rrotullimit) në drejtim të akrepave të orës. Nëse<0, то для определения положения одной из главных осей инерции для правой (левой) декартовой прямоугольной системы координат необходимо осьz kthehu në një kënd në drejtim të rrotullimit (në drejtim të kundërt) në drejtim të akrepave të orës.
Boshti maksimal bën gjithmonë një kënd më të vogël me atë të boshteve ( y ose z), në raport me të cilin momenti boshtor i inercisë ka një vlerë më të madhe (Fig. 6.9).
Boshti maksimal drejtohet në një kënd me boshtin(), if() dhe ndodhet në çerekun çift (tek) të boshteve, if().

Le të përcaktojmë momentet kryesore të inercisë dhe. Duke përdorur formulat nga trigonometria që lidhin funksionet,,, me funksionet,, nga formula (6.27) fitojmë
![]() ,
,